Wzór na wysokość trójkata równobocznego

Zajmijmy się trójkątem równobocznym. Jak sama nazwa mówi, jego boki są tej samej długości. Pamiętając o tych bokach bardzo łatwo możemy obliczyć miarę kąta wewnętrznego w tym trójkącie, gdyż każdy z trzech kątów jest tej samej miary.

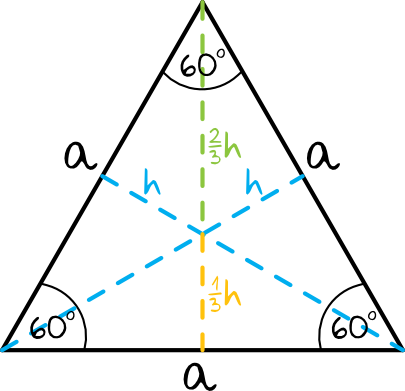
Jak wiesz, w każdym trójkącie znajdują się trzy wysokości. W trójkącie równobocznym (w przeciwieństwie do trójkątów równoramiennych i różnobocznych) każda z tych wysokości jest tej samej długości. Ponadto, zobacz poniższy rysunek. Czy widzisz zależność w tym, w jakim punkcie te wysokości się przecinają?

Jak widzisz, wysokości te przecinają się w taki sposób, że punkt przecięcia wysokości dzieli wysokość w stosunku 2 : 1, a więc na oraz na .

Jak więc obliczyć wysokość takiego trójkąta? Mamy kilka sposobów na wyznaczenie takiej wysokości.

I sposób wyznaczania wysokości w trójkącie równobocznym.
Spójrz na poniższy trójkąt. Jak widzisz, wysokość podzieliła ten trójkąt na dwa trójkąty prostokątne.

W obu tych trójkątach wysokość jest ta sama. Możemy ją obliczyć najprościej z twierdzenia Pitagorasa. Podpiszmy najpierw długości odpowiednich boków.

Założenia:
a > 0
h > 0

zapisujemy twierdzenie Pitagorasa

przerzucamy wiadome ( długości boków ) na prawo, a niewiadome ( wysokość ) na lewą stronę

podnosimy do drugiej potęgi

wyciągamy powtarzający się współczynnik po prawej stronie, a więc wyciągamy a w potędze drugiej przed nawias

odejmujemy od ciebie wartość z nawiasu powyżej, a następnie tę wartość zapisujemy przez a w potędze drugiej

zapisujemy całe wyrażenie na jednej kresce ułamkowej oraz pierwiastkujemy obustronnie

odrzucamy wysokość, która z równania kwadratowego wyszła nam ujemna, gdyż według założeń nasza wysokość musi być większa od zera

Takim oto sposobem wyprowadziliśmy wzór na wysokość w trójkącie równobocznym.

II sposób wyznaczania wysokości w trójkącie równobocznym.
Drugim sposobem obliczania wysokości trójkąta równobocznego, jest zastosowanie własności trójkąta o miarach kątów 30°, 60°, 90°. Jak wiesz, po podzieleniu trójkąta równobocznego otrzymujemy dwa trójkąty właśnie o tych miarach: 30°, 60°, 90°.

Jeśli dołożymy jeszcze jeden taki trójkąt obrócony o 180° poziomie, to otrzymalibyśmy cały trójkąt równoboczny. Narysujmy sobie jeszcze taki sam, ale odwrócony powyższy trójkąt w taki sposób, aby jego podstawą był bok a.


Traktując, że nasz bok jako 2a, otrzymalibyśmy taką zależność jak powyżej, a więc byłaby naszą wysokością trójkąta równobocznego o boku 2a.

Jeśli jednak bok naszego trójkąta to a (tak jest najczęściej), to po prostu każdą z wartości na trójkącie powyżej musimy podzielić na dwa. Tym samym otrzymujemy takie zależności jak poniżej:

Wysokością trójkąta równobocznego o boku a jest:

Takim oto sposobem wyprowadziliśmy wzór na wysokość w trójkącie równobocznym.

Spróbujmy teraz wykorzystać tę wiedzę praktyce. Zacznijmy od prostszych zadań.

zadanie 1
Oblicz wysokość trójkąta równobocznego o boku długości 12.

Rozwiązanie:

I sposób rozwiązania zadania (ze wzoru):

Rozwiązanie takiego zadania zaczynamy od wypisania danych, a następnie podstawiamy je do wzoru.

Dane:
a = 12

II sposób rozwiązania zadania

Rozwiązanie zadania zaczynamy wypisaniem danych. Następnie podstawiamy je do wzoru.

Zauważ, że tę wysokość możemy obliczyć również z twierdzenia Pitagorasa, gdzie:
a = 12

Założenia: h > 0

zapisujemy twierdzenie Pitagorasa

podstawiamy dane do równania

podnosimy do kwadratu dane nam wartości

redukujemy prawą stronę równania

pierwiastkujemy stronami

wyciągamy „całości”

Odpowiedź: Wysokość w trójkącie równobocznym o boku 12 wynosi .

zadanie 2
Oblicz wysokość trójkąta równobocznego o boku

Rozwiązanie:
Aby rozpocząć rozwiązywanie zadania otwartego zaczynamy od napisania danych. Oczywiście, te zadanie możemy również rozwiązać na dwa sposoby. Możemy od razu policzyć ze wzoru tę wysokość, możemy poprzez twierdzenie Pitagorasa obliczyć tę wysokość oraz możemy spojrzeć na wysokość w tym trójkącie jak wspólny bok dwóch trójkątów 30°, 60°, 90°. Ja wybrałam ten najszybszy sposób, a więc sposób ze wzorem, gdyż go doskonale znam.

Dane:
a =

Odpowiedź: Wysokość w trójkącie równobocznym o boku wynosi 3.

zadanie 3
Oblicz obwód oraz wysokość trójkąta równobocznego wiedząc, że jego pole wynosi .

Aby rozwiązać takie zadanie najpierw trzeba przypomnieć sobie wzór na pole trójkąta równobocznego. Oczywiście, pole te możemy liczyć a tradycyjnego wzoru na pole trójkąta, lecz wzór na pole trójkąta równobocznego zdecydowanie ułatwia nam zadanie. Na samym początku tego artykułu jest napisany wzór na pole trójkąta równobocznego, którym jest: . Jak widzisz, potrzebna nam jest tutaj tylko znajomość długości boku trójkąta, aby policzyć jego pole. Oczywiście, ten wzór łatwo możemy wyprowadzić, podstawiając wcześniej wyprowadzoną wysokość do tego wzoru:

ten wzór musimy przekształcić w taki sposób, aby wyznaczyć a, a następnie obliczymy obwód i wysokość tego trójkąta.

Założenia:
a > 0

Usuwamy mianownik mnożąc obustronnie przez 4

Obustronnie dzielimy przez pierwiastek z trzech

Pierwiastkujemy stronami

Otrzymujemy wynik

Podstawiamy nasz bok do wzoru na obwód trójkąta równobocznego. Wzór ten to nic innego jak bok trójkąta pomnożony razy 3.

Podstawiamy nasz bok do wzoru na wysokość trójkąta równobocznego.

Odpowiedź: Obwód tego trójkąta to 6, a jego wysokość to .