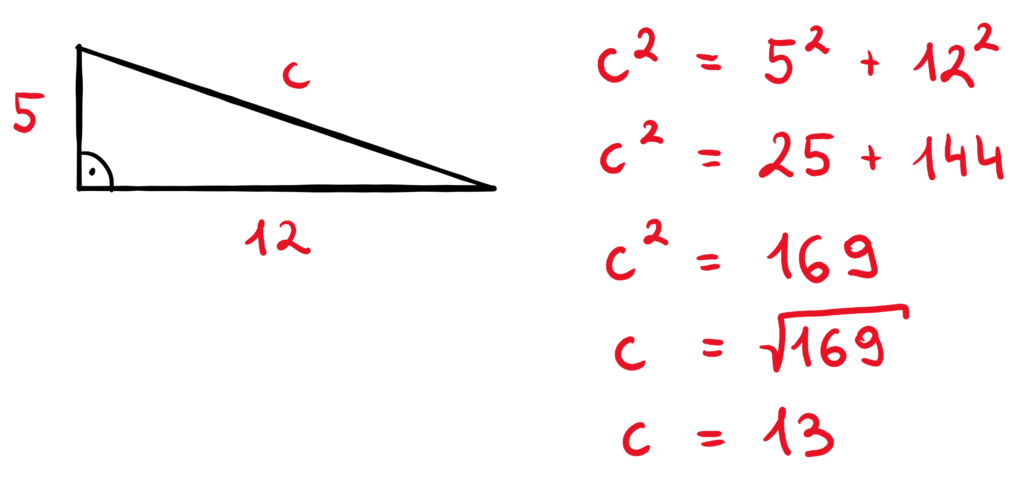Wzory matematyczne klasa 8

Najważniejsze wzory matematyczne klasa 8

1.Geometria płaska
a)Kwadrat
Aby obliczyć pole kwadratu możemy skorzystać ze wzoru:
P=a*a

Oprócz tego przydatny jest również wzór na obwód:
Ob=4a
Bardzo pożytecznym wzorem jest również wzór na przekątną kwadratu
d=a

b)prostokąt
Aby obliczyć pole prostokąta możemy skorzystać ze wzoru:
P=a*b

Wzór na obwód:
Ob.=2a+2b

c)trójkąt
Aby obliczyć pole trójkąta możemy skorzystać ze wzoru:
P= *a*h
Wzór na obwód:
Ob=a+b+c
*Twierdzenie pitagorasa
a +b =c

Z tego twierdzenia wynika iż a i b to długości przyprostokątnych, które są bokami trójkąta, które leżą bezpośrednio przy kącie prostym;
c to długość przeciwprostokątnej, który położony jest naprzeciwko kąta prostego.

Trójkąt pitagorejski
Trójkąt o bokach wyrażonych liczbami naturalnymi a, b, c, które spełniają warunek: a2+b2=c2.
Żeby odnaleźć trójkąty pitagorejskie, można posłużyć się wzorem:
a=2n+1
b=2n(n+1)
c=2n +2n+1
Trójkąt egipski
Jedyny trójkąt, który spełnia warunek a2+b2=c2, a przy ma boki o długościach odpowiadających kolejnym liczbom naturalnym: 3, 4 i 5.
Przykład 1
Oblicz długość przeciwprostokątnej:

Warunki stworzenia trójkąta:
Aby z trzech odcinków skonstruować trójkąt, najdłuższy z tych odcinków musi być krótszy niż suma długość dwóch pozostałych.
Własności trójkąta 30,60,90 (stopni)

Długość boku na przeciwko kąta 60 stopni wynosi a .
Długość boku na przeciwko kąta prostego wynosi 2a.
Własności trójkąta 45,45,90 (stopni)

Długość boku na przeciwko kąta prostego wnosi a

Natomiast przyprostokątne są równe.
Trójkąt równoboczny
Pole:
P=
Obwód:
Ob=3a
Wysokość:
h=

d)Romb
Pole:
P=a*h
Bok razy wysokość
Lub jeśli w zadaniu mamy podaną długość przekątnych:
P= *d*f
d, f- przekątne

e)Równoległobok
Pole:
P=a*h
Obwód:
O=2a+2b
f)Koło
Pole:
P=
Obwód:
O=

2.Stereometria
a)Sześcian
Pole:
P=6a

Objętość
V=a
Przekątna podstawy sześcianu:
a
Przekątna sześcianu:
a

b) Prostopadłościan
Objętość:
V=a*b*c
Pole:
P=2(ab +ac+ bc)