Zbiór

Jednym z pierwotnych pojęć w matematyce jest zbiór. Możesz wyobrazić sobie, że jest to taki worek, w którym są dane elementy. Przyjęło się, że nazwy zbiorów określamy wielkimi literami. W zbiorach zazwyczaj mamy wartości. Przykładowo:

Na zbiorach możemy wykonywać wiele działań.

ZBIORY MOŻEMY DO SIEBIE DODAWAĆ

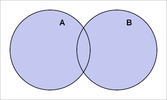
Przede wszystkim sumowanie, czy też dodawanie zbiorów oznaczamy symbolem: . Po dodaniu do siebie zbioru A oraz zbioru B, otrzymaliśmy ich sumę, która jest przedstawiona na grafice poniżej. Grafika ta ilustruje nam sumę zbiorów A oraz B poprzez diagram Venna.

Ćwiczenie:
Dodaj do siebie zbiór A oraz zbiór B.

Jak widzisz, powtarzającym się elementem jest wartość 1. Co ważne, w nowym zbiorze każda wartość występuje tylko raz, co oznacza, że:

ZBIORY MOŻEMY OD SIEBIE ODEJMOWAĆ

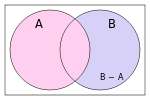
Operację, w której są odejmowane wzory nazywamy różnicą. Co ważne, w odejmowaniu kolejność ma znaczenie, dlatego zwróć szczególną uwagę na to, który zbiór od którego masz odjąć.

Różnicę określamy symbolem: „”.

Ćwiczenie: Wykonaj operację: A B.
A = { 1, 2, 5}
B = {1, 3, 4}

Od zbioru A musimy odjąć wszystkie wartości, które są te same co w zbiorze B. W obu zbiorach powtarza nam się 1, dlatego też wynikiem tej różnicy jest:
A B = {2, 5}

Ćwiczenie: Wykonaj operację: B A.
A = { 1, 2, 5}
B = {1, 3, 4}

W tym zadaniu będziemy postępować tak jak powyżej, tyle tylko, że od zbioru B będziemy odejmować zbiór A, a więc:

B A = {3, 4}

MOŻEMY WYKONYWAĆ OPERACJĘ „ILOCZYN” NA ZBIORACH

Najczęściej pewnie będziesz spotykać się z określeniem części wspólnej. Gdy mamy wykonać iloczyn zbiorów, to musimy znaleźć te elementy, które znajdują się zarówno w zbiorze A jak i w zbiorze B. Iloczyn oznaczamy symbolem: . Graficznie wygląda to o tak:

Ćwiczenie: Wykonaj operację: .
A = { 1, 2, 5}
B = {1, 3, 4}

Tylko jedynka powtarza się zarówno w zbiorze A jak i w zbiorze B.

Oczywiście, na zbiorach możemy wykonywać wiele bardziej skomplikowane operacje. Najważniejsze własności działań na zbiorach są przedstawione poniżej.

Przykład 1
Oblicz , gdzie A = { 1, 2, 3, 4 }, B = { 1, 3, 5}, C = { 3, 5, 9}

W tym rozwiązaniu użyłam wyżej pokazanych własności. Oczywiście, każdy mógł inaczej podejść do rozwiązania tego zadania. Mogliśmy nie używać tych wszystkich własności, dzięki czemu nasze rozwiązanie byłoby dużo krótsze.